java实现顺序存储二叉树

存储二叉树时，我们一般都用的是数组，不过在访问的时候是通过数组的下标来模拟访问！

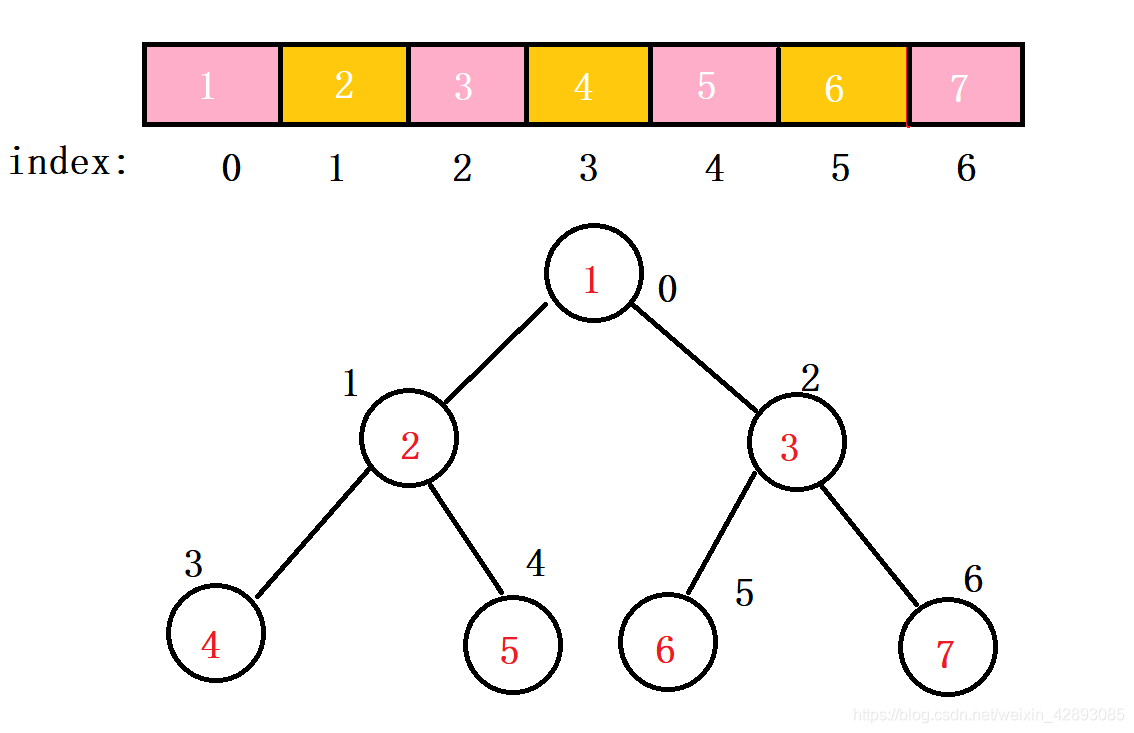
使用数组存放时只能从0开始存储，但是我们可以通过一定的规则对数组进行遍历就可以得到二叉树的的遍历的结果，下面我们先看一个遍历的规则：

顺序存储二叉树的特点：（这里的n指的是元素当前的索引值 ）
1.顺序二叉树通常只考虑完全二叉树
2.第n个元素的左子节点为： 2*n + 1
3.第n个元素的右子节点为： 2 *n + 2 (因为它是右子树所以在左子树的基础上加1)
4.第n个元素的父节点为：(n - 1)/2

下面我先给大家举几个栗子：

比如我要找3的左子树，那么它的索引就为2，通过计算左子树的公式：2 * 2 +1 = 5，它的左子树对应的索引 值 就为5，

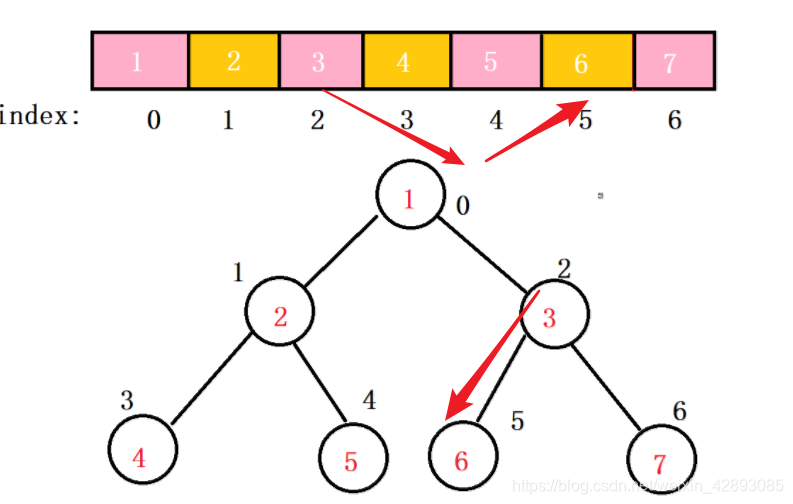
如果我们一直按照这样的规则遍历数组，就可以实现二叉树的先序、中序、后序遍历：

下面我们上代码来就明：

public class ArrayBinaryTreeDemo {

    public static void main(String[] args) {

        int[] arr = {1,2,3,4,5,6,7};

        ArrayBinaryTree arrayBinaryTree = new ArrayBinaryTree(arr);

        System.out.println("先序遍历后的数组为：");
        arrayBinaryTree.preOrder();
        System.out.println();

        System.out.println("中序遍历后的数组为：" );
        arrayBinaryTree.middleOrder();
        System.out.println();

        System.out.println("后序遍历后的数组为：");
        arrayBinaryTree.postOrder();
    }
}

//编写一个ArrayBinaryTree，实现顺序存储二叉树的遍历
class ArrayBinaryTree{
    private int[] arr;//存储数据节点的数组

    public ArrayBinaryTree(int[] arr) {
        this.arr = arr;
    }

    //重载preOrder方法,在main中只调用无参构造就可以了，使用方便
    public void preOrder(){
        this.preOrder(0);
    }

    public void middleOrder(){
        this.middleOrder(0);
    }

    public void postOrder(){
        this.postOrder(0);
    }
    //编写一个方法，完成顺序存储二叉树的一个前序遍历
    /**
     * 前序存储二叉树遍历
     * @param index 数组的下标
     */
    public void preOrder(int index){
        //如果数组为空，或者arr.lenght = 0
        if (arr == null || arr.length == 0) {
            System.out.println("数组为空，不能按照二叉树的前序遍历");
        }

        //输出当前这个元素
        System.out.print(arr[index] + "\t");
        //向左递归遍历
        if (index * 2 + 1 < arr.length) {
            preOrder(2 * index + 1);
        }

        //向右递归遍历
        if ((index * 2 + 2) < arr.length) {
            preOrder(2 * index + 2);
        }
    }

    /**
     * 中序存储二叉树遍历
     * @param index
     */
    public void middleOrder(int index){
        if (arr == null || arr.length == 0) {
            System.out.println("数组为空，不能按照中序遍历的方式遍历！");
        }
        if (index * 2 + 1 < arr.length) {
            middleOrder(2 * index + 1);
        }
        System.out.print(arr[index] + "\t");
        if (index * 2 + 2 < arr.length) {
            middleOrder(2 * index + 2);
        }
    }

    /**
     * 后序存储二叉树遍历
     * @param index
     */
    public void postOrder(int index){
        if (arr == null || arr.length == 0) {
            System.out.println("数组为空，不能按照后序遍历的方式遍历！");
        }
        if (index * 2 + 1 < arr.length) {
            postOrder( 2 * index + 1);
        }
        if (index * 2 + 2 < arr.length) {
            postOrder(2 * index +2);
        }
        System.out.print(arr[index] + "\t");
    }
}

运行结果

我们就成功的使用公式实现了二叉树的先序、中序、后序的遍历，如果本文中有哪个地方有误，希望大家多多指正！